Силовые поля в молекулярной динамике

Молекулярная динамика (МД) исторически складывалась как прикладная область — многие ключевые методы были разработаны так, чтобы стать частью прикладного программного обеспечивания. Рассмотрение ведётся со стороны программных пакетов для МД.

1 Классические силовые поля

МД требует явного задания вида потенциалов, описывающих взаимодействия атомов, этот потенциал определяется вкладом двух составляющих: \[ U = U_\text{ков.} + U_\text{неков.}, \] где терм \(U_\text{ков.}\) отвечает взаимодействию связанных химической связью атомов, а \(U_\text{неков.}\) — взаимодействию между далёкими атомами в одной молекуле или атомами в разных молекулах. Это деление обусловлено, во-первых, их видом¹, и, во-вторых, принципами, по которым оцениваются численные параметры, входящие в их выражения.

¹ ковалентные проявляются во взаимодействии химических связей, валентных углов и т.д., нековалентные действуют через пространство, убывают на расстоянии и суммируются по принципу «каждый с каждым»

Описание атома в МД весьма формально: достаточно задать выражение потенциалов взаимодействий и значения численных параметров этих уравнений. Для группировки численных параметров СП вводят т.н. типы атомов: например, в СП GAFF (⊞ 1) для алифатического \(sp^2\) атома углерода имеется тип атома c2, а для ароматического — ca.

Нековалентные взаимодействия обуславливают вторичную и более высокие порядки структуры макромолекул. Силовые поля, призванные описывать большой спектр химически разнородных молекул, как правило, уступают более специализированным СП. Таковые имеются для белков, нуклеиновых кислот, липидов и сахаров². В противовес им ставятся СП для описания малых молекул, например, лекарственно-подобных или воды.

² поскольку природные полимеры и липиды склонны образовывать структуры высших порядков (которые для многих задач МД критически важно воспроизводить с высокой точностью) и также содержат лишь небольшое число уникальных фрагментов

Table 1: Классические силовые поля

Пакет ПО	Силовое поле	Типы молекул
AMBER3	ff19SB4 Tian et al. (2020), ff14SB	белки
AMBER	GAFF5, GAFF2	малые орг. молекулы
AMBER	lipids21, lipid14 Dickson et al. (2014)	липиды
GROMACS6	GROMOS7	белки
CHARMM8	CHARMM27	белки и липиды
CHARMM	CGenFF9	малые молекулы
BOSS10	OPLS11	орг. молекулы

³ Assisted Model Building and Energy Refinement

⁴ Force Field Backbone and Side chain

Tian, Chuan, Koushik Kasavajhala, Kellon A. A. Belfon, Lauren Raguette, He Huang, Angela N. Migues, John Bickel, et al. 2020. “ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained Against Quantum Mechanics Energy Surfaces in Solution.” Journal of Chemical Theory and Computation 16 (1): 528–52. https://doi.org/10.1021/acs.jctc.9b00591.

⁵ General AMBER Force Field

Dickson, Callum J., Benjamin D. Madej, Åge A. Skjevik, Robin M. Betz, Knut Teigen, Ian R. Gould, and Ross C. Walker. 2014. “Lipid14: The Amber Lipid Force Field.” Journal of Chemical Theory and Computation 10 (2): 865–79. https://doi.org/10.1021/ct4010307.

⁶ GROningen MAchine for Chemical Simulations

⁷ GROningen MOlecular Simulation

⁸ Chemistry at HARvard Molecular Mechanics

⁹ CHARMM General Force Field

¹⁰ Biochemical and Organic Simulation System

¹¹ Optimized Potentials for Liquid Simulations

Разработка параметров

Оценка параметров атомов СП производится по данным квантово-механического (КМ) моделирования с опорой на экспериментальные данные. Из серии КМ расчётов, проведённых для разных искажённых геометрий одной молекулы, можно сначала определить потенциальную энергию различных конформаций, а затем найти оценку параметров жёсткости длины связи и её валентных углов в выражениях закона Гука, и периодических потенциалов взаимодействия, описываемые рядами.

Несколько иначе обстоит дело с первичной оценкой параметров нековалентных взаимодействий, их получают из множества симуляций чистых жидкостей (алканов, спиртов, амидов и т.д.), нацеленных на воспроизведение макроскопических свойств¹², например, теплот испарения и \(\Delta_\text{vap} H\) и плотностей. Полученные на каждом этапе оценки вовлекаются в дальнейшие расчёты и многократно и последовательно уточняются, чтобы прийти к согласию с экспериментальными данными.

¹² тогда как для ковалентные взаимодействия первоначально аппроксимируются на атомных масштабах

Для уточнения параметров ковалентных взаимодействий результаты расчётов также приводят к соответствию с экспериментальными данными:

• совпадению частот колебаний в ИК-спектрах;
• воспроизводимости экспериментальных геометрий;
• воспроизведению конформаций (распределений величин углов, длин связей, межатомных расстояний по данным РСА;

также параметры, рассчитанные в вакууме, переоцениваются в непрерывной среде.

И на микро-, и на макроскопические свойства веществ влияют как ковалентные, так и нековалентные взаимодействия, однако при разработке СП итеративный подход с последовательным уточнением сначала одних, затем других параметров оказывается проще. Это не в полной мере относится к параметрам молекулы воды. В нормальной случае природные молекулы моделируют в водной среде, т/е доля «водных» атомов в системе сверху ограничена только 100%ми. Вклад растворителя в ТД свойства системы пропорционален его доле и может быть решающим, также он играет большую роль при воспроизведении экспериментальных данных.

Учёт анизотропии

Представление атома как точечного заряда не всегда адекватно описывает реальное положение вещей. Приведём несколько примеров.

1. Атом кислорода в молекуле воды обладает двумя неподелёнными электронными парами, их наличие можно довольно точно учесть, если к описанию молекулы воды тремя материальными зарядами (по одному на каждый атом) добавить два нематериальных отрицательных задяда, поместив их позади атома кислорода (см. § 2).
2. Атомы тяжёлых галогенов \(\text{X}\) обладают высокой поляризуемостью, в некоторых галогенпроизводных \(\text{RX}\) электронное окружение атома галогена может быть смещено к заместителю \(\text{R}\), приводя к обнажению небольшого положительного заряда (т.н. \(\sigma\)-дырки) на атоме галогена со стороны Lu et al. (2012), противоположной связи \(\text{R-X}\). Этот положительный заряд может участвовать в электростатических взаимодействиях с другими атомами, образуя галогеновые связи (по аналогии с водородными). \(\sigma\)-Дырки могут быть описаны добавлением небольшого положительного заряда в нужною область пространство вблизи атома галогена.
3. По аналогичным причинам \(\pi\)-облака могут участвовать в координационных \(\pi\)-взаимодействиях Hunter and Sanders (1990), которые можно учесть добавив 2 отрицательных заряда к каждому атому углерода.

Lu, Yunxiang, Yingtao Liu, Zhijian Xu, Haiying Li, Honglai Liu, and Weiliang Zhu. 2012. “Halogen Bonding for Rational Drug Design and New Drug Discovery.” Expert Opinion on Drug Discovery 7 (5): 375–83. https://doi.org/10.1517/17460441.2012.678829.

Hunter, Christopher A., and Jeremy K. M. Sanders. 1990. “The Nature of .pi.-.pi. Interactions.” Journal of the American Chemical Society 112 (14): 5525–34. https://doi.org/10.1021/ja00170a016.

Более продвинутые подходы для учёта анизотропии обсуждаются в § 3.1.

RESP

Заряды на атомах сильно зависят от их связей с другими атомами, поэтому зачастую СП не содержат параметров заряда, требуя их явного указания. Для расчёта зарядов применяется метод RESP¹³ Bayly et al. (1993). Приведём его кратное описание.

¹³ Restrained Electrostatic Potential

Bayly, Christopher I., Piotr Cieplak, Wendy Cornell, and Peter A. Kollman. 1993. “A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model.” The Journal of Physical Chemistry 97 (40): 10269–80. https://doi.org/10.1021/j100142a004.

1. Для целевой молекулы должна быть найдена оптимальная геометрия, для сложных органических молекул рекомендуется использовать приближение теории возмущений Мёллера – Плессе 2го порядка (MP2).
2. Рассчитывается значение электростатического потенциала \(V_i\) (в базисе 6-31G*) в разных точках \(i\) на небольшом удалении от молекулы.
3. Методом наименьших квадратов находятся оценки зарядов на атомах:

   • Записывается выражение оценки потенциала \(\hat V_i\) через заряды: \[ \hat V_i = \sum_j \dfrac{\hat q_j}{r_{i,j}} \qquad i, j = 1..N, \] где \(\hat q_j\) — искомая оценка заряда для атома \(j\), \(r_{i,j}\) — расстояние от атома \(j\) до точки \(i\) измерения потенциала \(V_i\).

   • Определяется выражение целевой функции для метода наименьших квадратов: \[ \chi^2 = \underbrace{\sum_i (V_i - \hat V_i)^2}_{\chi^2_\text{esp}} + \underbrace{a \sum_j (\hat{\hat{q}}_j - \hat q_j)^2}_{\chi^2_\text{rstr}} \to \min_{\hat q_1, \cdots, \hat q_N}, \] где \(\hat{\hat{q}}_j\) — грубая оценка искомого заряда, используемая для регуляризации¹⁴, \(a\) — числовой коэффициент, \(\chi^2_\text{esp}\) и \(\chi^2_\text{rstr}\) — квадратичные невязки на величину потенциала и регуляризацию.

   • Ищется экстремум целевой функции, отвечающий минимуму: \[ \frac{\partial \chi^2}{\partial \hat{q}_j} = \frac{\partial \chi^2_\text{esp}}{\partial \hat{q}_j} + \frac{\partial \chi^2_\text{rstr}}{\partial \hat{q}_j} = 0 \qquad j = 1..N. \] Исходя из симметрии молекулы задаются ограничения на эквивалентность атомов \(k\) и \(l\): \(\hat q_k = \hat q_l\). Полученные оценки \(\hat q_j\) используются как параметры заряда атомов в ходе МД.

¹⁴ штраф за отклонение оценок от некоторых грубых, но разумных значений

Различия классических силовых полей

Принципы, лежащие в основе построения силовых полей, во многом близки, однако стоит отметить и различия Guvench and MacKerell (2008).

Guvench, Olgun, and Alexander D. MacKerell. 2008. “Comparison of protein force fields for molecular dynamics simulations.” Methods in Molecular Biology (Clifton, N.J.) 443: 63–88. https://doi.org/10.1007/978-1-59745-177-2_4.

1. В некоторых СП семейств OPLS, GROMOS и CHARMM неполярные атомы водорода, например, при алифатических атомах углерода, опускаются, т.е. группа \(\text{-CH}_2\text{-}\) представляется одним псевдоатомом углерода, его масса, заряд и другие параметры разработаны так, чтобы в МД походить на метиленовую группу. С одной стороны это ухудшает качество модели, с другой позволяет не тратить время на расчёт иногда не слишком важных взаимодействий. Сообщается, что в этом подходе число вычислений может уменьшаться до 10 раз. (Kmiecik et al. 2016, с. 7903)

2. В СП для описания плоских групп вводятся псевдоторсионные углы \(\xi\), призванные удерживать 4 произвольных атома в одной плоскости. В полях семейств AMBER и OPLS-AA потенциал, накладываемый на этот угол имеет периодический характер (Amber 2021 Reference Manual 2021, с. 275): \[ U \propto 1 + \cos (n (\xi - \bar \xi)) \qquad n = 2, \] в полях CHARMM и GROMOS — вводится отдельный параболический потенциал аналогично с длинами связей и валентными углами (Bauer, Hess, and Lindahl 2022, ур. 196): \[ U \propto (\xi - \bar \xi)^2. \]

3. СП семейства CHARMM имеют дополнительный терм — т.н. потенциал Юри-Брэдли “Potential Energy Functions” (n.d.). Для описания напряжения, возникающего для тройки ковалентно связанных атомов \(\text{X-Y-Z}\), вводится 2 параболических потенциала: первый, на величину валентного угла \(\theta = \widehat{\rm{X, Y, Z}}\), второй на расстояние \(r_t = |\bf r_{\rm X} - \bf r_{\rm Z}|\) между терминальными атомами в тройке. Таким образом, потенциал валентного угла \[ U_a = k_\theta (\theta - \bar \theta)^2 + k_t (r_t - \bar r_t)^2, \] добавление новых степеней свободы в СП мотивировано попыткой лучшего описания колебательный спектров.

4. Вид потенциала взаимодействия двух ковалентно несвязанных атомов \(\text{X}\) и \(\text{Y}\) задаются уравнением Ленарда — Джонса. Его можно переформулировать через параметры глубины потенциальной ямы (энергии взаимодействия) \(\epsilon_{\ce X, \ce Y}\) и соответствующего ей расстояния \(r^{\min}_{\ce X,\ce Y}\): \[ U_\text{LJ}(r) = \epsilon_{\ce X, \ce Y} \left\{ \left(\dfrac{r^\text{min}_{\ce X, \ce Y}}{r}\right)^{12} - 2 \left(\dfrac{r^\text{min}_{\ce X, \ce Y}}{r} \right)^6 \right\}. \] Если природа взаимодействующих атомов идентична (\(\text{X} = \text{Y}\)), то параметры \(\epsilon_{\ce X, \ce X}\) и \(r^{\min}_{\ce X, \ce X}\) берутся непосредственно из СП для соответствующего \(\text{X}\) типа атома, если \(\text{X} \ne \text{Y}\), то параметры попарных взаимодействий необходимо вычислять. В силовых полях OPLS-AA и GROMOS они вычисляются как среднее геометрическое \[ \epsilon_{\ce X,\ce Y} := \sqrt{\epsilon_{\ce X, \ce X} \cdot \epsilon_{\ce Y,\ce Y}}, \qquad r^{\min}_{\ce X,\ce Y} := \sqrt{r^{\min}_{\ce X,\ce X} \cdot r^{\min}_{\ce Y,\ce Y}}, \] в силовых полях CHARMM и AMBER аналогично вычисляется \(\epsilon_{\ce X,\ce Y}\), а \(r^{\min}_{\ce X,\ce Y}\) как среднее арифметическое: \[ r^{\min}_{\ce X,\ce Y} = \dfrac 1 2 ( r^{\min}_{\ce X,\ce X} + r^{\min}_{\ce Y,\ce Y} ). \]

5. Поскольку параметры потенциала вычисляются для пар разных атомов по весьма простым правилам, для лучшей воспроизводимости экспериментальных барьеров вращения торсионных углов в разных СП вводятся масштабирующие множители к 1-4 взаимодействиям. В AMBER величина кулоновских и леннардджонсоновских взаимодействия умножаются на \(1 / 2\) и \(5 / 6\) соответственно, в OPLS-AA оба на \(1 / 2\), GROMOS и CHARMM применяют разные корректировки к разным парам атомов.

6. Для лучшего описания пар торсионных углов \(\alpha\) и \(\beta\) в CHARMM (и затем в других СП) появились CMAP¹⁵ — дискретные энергетические поправки, представляющий собой матрицы из чисел для всех значений пары двугранных углов \(\alpha\) и \(\beta\) с шагом \(15^\circ\), т.е. \[ (\delta U)_{i,j} \quad \colon \quad \alpha_i, \beta_j = -180^\circ, -165^\circ, \cdots, +165, +180^\circ, \] на основе этой сетки конструируется непрерывная функция, которая используется для коррекции энергии Bjelkmar et al. (2010).

Amber 2021 Reference Manual. 2021.

Bauer, Paul, Berk Hess, and Erik Lindahl. 2022. “GROMACS 2022 Manual.” Zenodo. https://doi.org/10.5281/zenodo.6103568.

“Potential Energy Functions.” n.d. Accessed April 29, 2022. https://www.ks.uiuc.edu/Research/namd/2.9/ug/node22.html.

¹⁵ Correction MAP

Bjelkmar, Pär, Per Larsson, Michel A. Cuendet, Berk Hess, and Erik Lindahl. 2010. “Implementation of the CHARMM Force Field in GROMACS: Analysis of Protein Stability Effects from Correction Maps, Virtual Interaction Sites, and Water Models.” Journal of Chemical Theory and Computation 6 (2): 459–66. https://doi.org/10.1021/ct900549r.

2 Модели воды

Молекула воды обладает высоким дипольным моментом (в следствие анизотропии, вызванной неподелёнными электронными парами, и высокой электроотрицательностью кислорода) и способна образовывать 4 водородные связи: 2 будучи донором, 2 как акцептор. Помимо этого, объёмные электронные облака атома кислорода в окружении молекул с высоким дипольным моментом подвергаются поляризации. Классические СП не могут учесть явно ни наличие неподелённых электронных пар, ни поляризацию, поэтому для представления молекул воды были разработаны специальные подходы Onufriev and Izadi (2018).

Onufriev, Alexey V., and Saeed Izadi. 2018. “Water Models for Biomolecular Simulations.” WIREs Computational Molecular Science 8 (2): e1347. https://doi.org/10.1002/wcms.1347.

TIP\(n\)P

Как было сказано ранее, обычно в МД большая часть атомов системы относится к растворителю, поэтому существует большой соблазн оптимизировать его модель так, чтобы большая часть вычислительных ресурсов не уходила на рассчёт взаимодействий между молекулами воды. Наиболее часто используемое семейство СП для описания воды — TIP\(n\)P¹⁶, где \(n = 2..6\) — число материальных точек, аппроксимирующих электронную плотность молекулы воды; взаимное расположение этих точек фиксировано, т.е. жёсткость связей и валентных углов не берётся в расчёт для экономии вычислительных ресурсов; в межмолекулярном взаимодействии участвует только атом кислорода, который имеет потенциал Ленарда — Джонса, другие частицы в системе его не имеют¹⁷.

¹⁶ Transferable Intermolecular Potential with \(n\) Points

¹⁷ в более общих реализациях TIP\(n\)`P$, потенциал можно задавать для всех частиц в молекуле

Jorgensen, William L. 1981. “Quantum and Statistical Mechanical Studies of Liquids. 10. Transferable Intermolecular Potential Functions for Water, Alcohols, and Ethers. Application to Liquid Water.” Journal of the American Chemical Society 103 (2): 335–40. https://doi.org/10.1021/ja00392a016.

¹⁸ иными словами, анизотропии электронной плотности

Jorgensen, William L., Jayaraman Chandrasekhar, Jeffry D. Madura, Roger W. Impey, and Michael L. Klein. 1983. “Comparison of Simple Potential Functions for Simulating Liquid Water.” The Journal of Chemical Physics 79 (2): 926–35. https://doi.org/10.1063/1.445869.

Первой моделью была TIP3P Jorgensen (1981), в ней молекула воды описывается тремя зарядами, находящимися в центре трёх её атомов. Затем для учёта квадрупольного момента¹⁸ была предложена Jorgensen et al. (1983) модель TIP4P, в которой вводится четвёртый заряд, помещаемый близко к условному центру молекулы. Наконец, появилась модель TIP5P, в которой каждой неподелённой паре кислорода приписывается нематериальный заряд. Существуют также TIP2P, в которой молекула воды описывается простым диполем, и TIP6P — комбинация подходов TIP5P и TIP4P, т.е. 2 дополнительных заряда аппроксимируют электронную плотность позади атома кислорода и 1 — около геометрического центра.

Несмотря на то что усложнение модели приводит к повышению её точности и лучшему описанию экспериментальных данных, модель воды TIP3P сейчас используется наиболее часто ввиду того, что при достаточно точном описании позволяет существенно сократить затраты на расчёты.

В подходе к разработке СП (§ 1.1), когда результаты расчётов итеративно подводят под согласие с термодинамическими или спектроскопическими данными, параметры СП неизбежно зависят от выбранной модели воды, что приводит к концепции самосогласованности силовых полей: поскольку все числовые параметры находятся в сложной зависимости друг от друга, рекомендуется использовать только те наборы параметров, которые использовались при создании СП и рекомендуются его разработчиками. Например, если СП для молекулы белка было разработано для использования с моделью воды TIP3P, то использование модели TIP6P в нормальном случае приведёт к ухудшению результатов, поскольку СП белка было оптимизировано для работы с более простой моделью растворителя.

OPC

Геометрия молекулы воды в моделях TIP\(n\)P берётся из геометрии молекулы в газовой фазе. Иной подход был использован при разработке модели OPC¹⁹, геометрия которой была оптимизирована с одним лишь ограничением — в группе симметрии \(C_{2v}\). Как и TIP4P молекула воды в OPC состоит из 4х точек: условного атома кислорода, создающего потенциал Леннарда — Джонса, но не обладающего зарядом, и 3х точек (условно, двух водородов и одного кислорода), аппроксимирующих электростатический потенциал, но не имеющих параметров вандерваальсовых взаимодействий. Таким образом, заряд атома кислорода находится не в его центре. Модель OPC хорошо воспроизводит рассчитанный квантовыми методами распределение заряда и физические свойства жидкой воды и в большинстве случаев показывает себя лучше, чем TIP3P. Разработчики СП ff19SB (семейство AMBER) использовали OPC при разработке и рекомендуют использовать при расчётах.

¹⁹ Optimal Point Charges

3 Неклассические силовые поля

Поляризуемые силовые поля

На атомных масштабах представление атома в виде материальной точки может оказаться слишком простым. Тот факт, что электронная плотность динамически подстраивается под влияние окружающего поля и атомного ядра приводит к явлению анизотропии, которое невозможно описать в рамках классических силовых полей. Для учёта этого эффекта разработан ряд подходов Jing et al. (2019), которые, однако, на практике применяются не очень часто ввиду того, что требуют бóльших вычислений, но с каждым годом использование этих методов становится всё более оправданным Baker (2015).

Jing, Zhifeng, Chengwen Liu, Sara Y. Cheng, Rui Qi, Brandon D. Walker, Jean-Philip Piquemal, and Pengyu Ren. 2019. “Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications.” Annual Review of Biophysics 48 (1): 371–94. https://doi.org/10.1146/annurev-biophys-070317-033349.

Baker, Christopher M. 2015. “Polarizable Force Fields for Molecular Dynamics Simulations of Biomolecules.” Wiley Interdisciplinary Reviews: Computational Molecular Science 5 (2): 241–54. https://doi.org/10.1002/wcms.1215.

Полная энергия электростатического взаимодействия \[ E_t = E_q + E_p, \] где \(E_q\) — сумма кулоновских потенциалов, \(E_p\) — работа по перераспределению индуцированных зарядов, вид которой (обычно квадратичный) в разных подходах различен.

Table 2: Поляризуемые силовые поля

силовое поле	метод	пакет ПО
AMBER	инд. диполи	AMBER
AMOEBA	инд. диполи	AMBER, TINKER, OpenMM
CHARMM-Drude	«заряды на пружинах»	AMBER, CHARMM, NAMD, GROMACS, OpenMM
CHARMM-FQ	колебл. заряды	CHARMM
SIBRA	инд. диполи	TINKER
ABEEM\(\sigma \pi\)	колебл. заряды	TINKER

Колеблющиеся заряды²⁰

В методе колеблющихся зарядов взаимодействие между атомами рассчитывается аналогично тому, как это реализовано в неполяризуемых СП. Отличие заключается в том, что частичные атомные заряды получают свои степени свободы в уравнении движения и могут перетекать по связям в молекулярном графе, причём это реализуется непосредственно в СП: заряду приписывается некоторая инертность (аналог массы), и заряд, участвуя во взаимодействиях, испытывает на себе влияние других зарядов и, соответственно, стремится выгодно перераспределиться в молекуле. \[ E_p := \sum_i (\chi_i q_i + \eta_i q_i^2), \] где \(\chi\) и \(\eta\) — электроотрицательность (\(\partial E_p / \partial q\)) и жёсткость (\(\partial^2 E_p / \partial q^2\)) соответственно. Этот подход применим только для описания поляризации, возникающей вдоль химической связи, и, например, не способен описать перераспределение электронной плотности в \(\pi\)-облаках ароматических колец.

²⁰ англ. fluctuating charges

²¹ англ. Drude oscillators или charges on springs

«Заряды на пружинах»²¹

В модели заряда на пружинах каждый атом представляется в виде пары зарядов: один находится в центре атома и обладает массой, а второй нематериальный заряд крепится к первому с помощью относительно короткой пружины жёсткость \(k\). В ходе расчёта заряд частиц остаётся постоянным, но его распределение в пространстве меняется вследствие того, что нематериальный заряд свободно перемещается относительно центрального на величину смещения \(\bf d\), подстраиваясь под внешнее поле (и создавая дипольный момент): \[ E_p := \dfrac 1 2 \sum_i k_i \bf d_i^2. \] В отличие от метода колеблющихся зарядов, в этом приближении делается попытка описания электронной плотности молекулы, а не просто перераспределения частичных зарядов.

Индуцируемые диполи

В методе индуцированного диполя каждому атому приписывается поляризуемость \(\alpha\) и динамически вычисляется индуцированный дипольный момент: \[ \mu = \alpha E, \] где \(E\) — напряжённость внешнего поля и \[ E_p = \frac{1}{2} \sum_i \frac{\boldsymbol \mu_i^2}{\alpha_i}. \] В этом подходе явным образом вводится новая сущность — диполь, соответственно СП должно включать термы для описания взаимодействий диполь—диполь и диполь—заряд.

Крупнозернистые²² силовые поля

Поляризуемые СП стремятся пожертвовать скоростью в пользу точности, но даже классические СП зачастую слишком ресурсозатратны для моделирования надмолекулярных систем: клеточных мембран, цепей нуклеиновых кислот и полисахаридов, и даже белков. В § 1.4 отмечалось, что неполярные атомы водорода для экономии вычислительных ресурсов могут опускаться, однако в подходе крупнозернистых (КЗ) полей — целые группы атомов упрощаются до одного псевдоатома Kmiecik et al. (2016).

Важной задачей является моделирования сворачивания белков, однако при текущей доступности ресурсов классическая МД ограничена размером системы и временем её моделирования, поэтому изучению этим методом поддаётся лишь малое множество объектов — небольшие быстро сворачивающиеся белки; появление КЗ СП обусловлено желанием перенести МД на масштабы и времена бóльших биологических систем.

Figure 1: Представление пептида в различных крупнозернистых подходах Kmiecik et al. (2016)

Kmiecik, Sebastian, Dominik Gront, Michal Kolinski, Lukasz Wieteska, Aleksandra Elzbieta Dawid, and Andrzej Kolinski. 2016. “Coarse-Grained Protein Models and Their Applications.” Chemical Reviews 116 (14): 7898–7936. https://doi.org/10.1021/acs.chemrev.6b00163.

На примере белков отметим ряд общих подходов, используемых при построении крупнозернистых силовых полей:

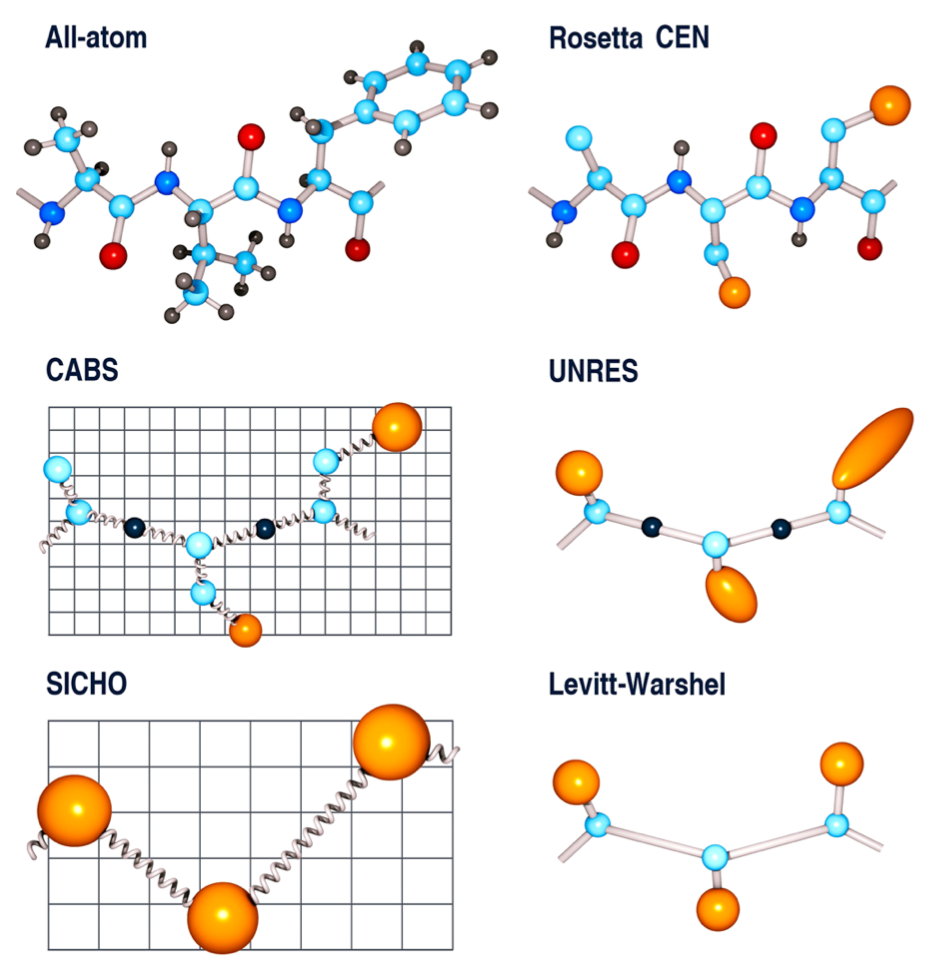
1. Группы атомов объединяются в один псевдоатом, так полипептидная цепь на разных уровнях детализации может представлять собой: а) полноатомную цепь с опущенными неполярными атомами водорода; б) идеализированную цепь, состоящую из «бусин»²³ (нескольких атомов, слитых в один псевдоатом) — аминокислотных остовов, к которым крепятся 2 типа бусин боковых остатков (полярные и неполярные); в) цель состоящую из одинаковых бусин. Так же возможно большое число промежуточных вариантов ⬟ 1.

2. Псевдоатомы параметризуется так, чтобы походить в МД на исходную группу. Для этого применяются два подхода. В первом: данные, полученные из моделирования бековой глобулы с классическим силовым полем, используются для разработки необходимых параметров, при этом используется итеративная процедура, в которой результат моделирования КЗ ансамбля последовательно подводится под воспроизведение свойств классического; в качестве целевой метрики может использоваться радиальная функция распределения \[ \rho (r) \propto \dfrac 1 {4 \pi r^2} \dfrac{\mathrm{d} N(r)}{\mathrm{d} r}, \] показывающая пространственное распределение числа частиц \(N\) на расстоянии \(r\) от выбранной точки²⁴, эта функция ёмко описывает порядок между частицами в системе. Во втором подходе не используются косвенные данные, полученные из ансамблей более точных моделей МД, вместо этого используются арсенал методов, применяемый при построении классических силовых полей: данные квантового моделирования и эксперимента.

3. Атомы в классических моделях существуют в непрерывном пространстве, КЗ модели могут вводить дискретные пространства, или решётки, т.е. атомы в них могут находиться только в конечном числе точек пространства, что значительно ускоряет время расчёта.

4. Длина связи между псеводоатомами в КЗ моделях может быть фиксированной, т.е. изменение конформации белка будет возможно только за счёт вращения вокруг связи.

5. Степени свободы валентных углов также могут ограничиваться, например, положение, которое боковая цепь занимает по отношению к основной цепи, может быть детерминированной функций от координат псевдоатомов, например, псевдоатом боковой группы может лежать на биссектрисе угла, образованного тремя атомами остова.

²³ англ. beads

²⁴ на практике может строиться гистограмма всех попарных расстояний между частицами в системе, полученное распределение и есть радиальная функция распределения

Следует подчеркнуть, что в КЗ подходах можно получать точные оценки свободной энергии, однако при оценке энтропийного вклада требуется внесение поправок для учёта меньшего числа частиц в системе.

²² от англ. coarse-grained force fields